Rc-цепи, 5 самых ходовых схем фильтров и их простой рассчет

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Переходные процессы в RС и RL — цепях.

Переходные процессы в электрических цепях возникают при включении или выключении э. д.с., а также при изменении одного или нескольких параметров цепи.

Переходные процессы в электрических линейных цепях описываются линейными дифференциальными уравнениями, составленными согласно правил Кирхгофа.

Рассмотрим переходные процессы в электрической цепи, изображенной на рис.2.

Р и с. 2 Р и с. 3

При включении RC — цепи под постоянное напряжение e (t) = U полагаем, что приt = 0, Uc = 0 (конденсатор незаряжен). Исходя из второго правила Кирхгофа, получаем:

Uc + UR = U0 или IR + Uc = U0 . (5)

Подставляя выражение I = c×dUc dtполучаем выражение вида

RC× dUc/dt + Uc = U0 .(6)

Решение этого дифференциального уравнения первого порядка можно записать в виде:

Uc = U0 × (1 — e-t/tc), (7)

где tc = RC —постоянная времени электрической цепи, равная промежутку времени, по истечении которого напряжение в цепи изменяется в e = 2,7 раз по сравнению U.

Ток заряда в RC—цепи при переходном процессе определяется

(I0 = c×dUc /dt).

Iз =(U0/R) × e-t/tc. (8)

Напряжение на активном сопротивлении (UR =Iз R)

UR = U0× e-t/tc. (9)

Анализ полученных временных зависимостей Uc(t)и Iз(t) в RC —цепи во время переходного процесса показывает, что с течением времени напряжение на конденсаторе Ucвозрастает, стремясь к U (рис.4), а ток убывает от значения, равногоUR , до нуля (рис. 5). При этом изменении напряжения на конденсаторе и тока в цепи при переходном режиме происходит тем быстрее, чем меньше постоянная времени цепи tc = RC .

Р и с. 4 Р и с. 5

Короткое замыкание RC— цепи, т. е. разряд конденсатора С на активное сопротивление R, можно описать уравнением:

Uc + UR = 0 ,(10)

где Ip = CdUc /dt ; UR = IpR ;

Получим однородное дифференциальное уравнение первого порядка:

Uc + RCdUc /dt = 0 , (11)

Решение этого уравнения имеет вид:

Uc = U0× e-t/tc , (12)

где U = Uc (0)

Для тока разряда можно записать

Ip = -(U0/R) × e-t/tc , (13)

а для напряжения UR — соответственно

UR = — U0× e-t/tc. (14)

Временные зависимости для тока и напряжения во время переходного процесса представлены на рис. 6, 7, из которых видно, что напряжение Uс и ток Ip убывают по экспоненциальным законам в соответствии с постоянной времени tc = RC .

Р и с. 6 Р и с. 7

Рассмотрим RL — цепь, изображенную на рис.3. При включении U под постоянное напряжение переходный процесс описывается дифференциальным уравнением:

UR + UL = U0 ,(15)

где UR = IзR ; UL = LdIз /dt;

т. е. IзR + LdIз /dt = U0 . (16)

Решение этого линейного дифференциального уравнения первого порядка является уравнением типа

Iз = U0/R(1 — e-t/tL), (17)

где tL = LR— постоянная времени RL — цепи, равная промежутку времени, по истечении которого ток в цепи изменяется в e = 2,7 раз по сравнению со своим исходным значением I. Напряжение переходного процесса на индуктивности L можно записать в виде

UL = LdIз /dt;

UL = U0 e-t/tL .(18)

Нарис. 8, 9 представлены динамические характеристики тока в цепи и напряжения UR , UL при переходном процессе. Во время переходного процесса ток в цепи постепенно возрастает от нуля до I = UR, в это время напряжение на индуктивности убывает от U = UL(0) до нуля.

Р и с. 8 Р и с. 9

При коротком замыкании RL — цепи, происходит разряд катушки индуктивности на активное сопротивление R.

Можно записать

UL + UR = 0, (19)

(L/R)(dIp/dt) + Ip = 0. (20)

Решение уравнения (20) имеет вид

Ip = (U0/R) e-t/tL. (21)

Соответственно

UL = — U0 e-t/tL , (22)

UR = U0 e-t/tL . (23)

Из анализа временных зависимостей тока и напряжений следует, что ток в RL — цепи уменьшается по экспоненциальному закону от I = UR до нуля. Аналогично изменяется и UL (рис. 10, 11).

Р и с. 10 Р и с. 11

Теоретически переходные процессы длятся неограниченно долго. Практически принято считать переходной процесс оконченным, если разность между изменяющейся величиной и ее предельным значением составляет 5%. Например, из выражения (3) имеем

t = tпер, Uc (tпер) = 0,95 U, 0,95 U = U (1- e—tпер/tc),

e—tпер/tc = 0,05; tпер = 3t (24)

где tпер — время переходного процесса.

1.2.2 Дифференцирующая (укорачивающая) и разделительная rc-цепи.

Дифференцирующей
цепью называют такую цепь, сигнал на
выходе которой имеет значения,
пропорциональные в каждый момент
производной от входного сигнала.
Следовательно,
.
КоэффициентКдолжен выражаться в
секундах, в противном случае размерность
левой и правой частей равенства не будет
одинакова. Идеальным дифференцирующим
устройством можно считать конденсаторСили катушкуL.
Например, при использовании конденсатораСможно считать входным сигналом
напряжение на нём,
а выходным – токв цепи. Эти переменные связаны известным
соотношением,
т.е. ток в цепи пропорционален производной
от входного напряжения. Однако использовать
эту схему для практических целей нельзя,
так как она не содержит элемента, который
обеспечивал бы какую-либо регистрацию
значений тока, измерение его значений.

Для того чтобы
получить выходной сигнал в форме, удобной
для наблюдения или регистрации, в цепь
последовательно включают токочувствительный
прибор с внутренним сопротивлением R.
В простейшем случаи это может быть
резисторR. Напряжение
на котором пропорционально току.

Рассмотренная
RC-цепочка может
выполнять функции как дифференцирующей
(укорачивающей) при,
так и разделительной цепи, если.

На рис.1.11 показаны
графики напряжени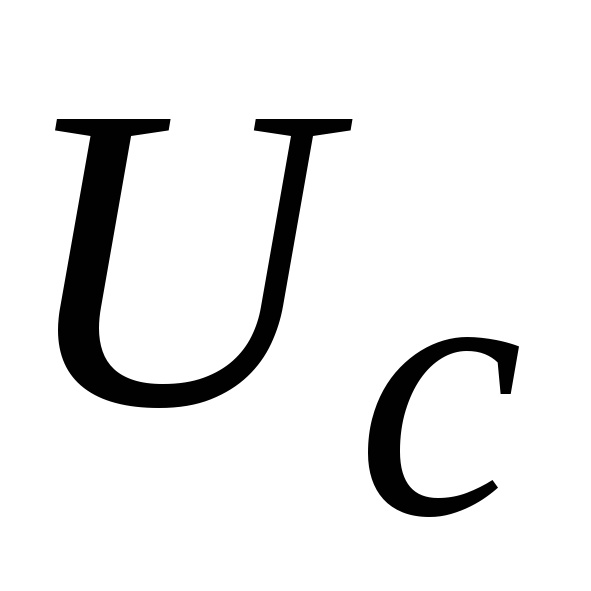й
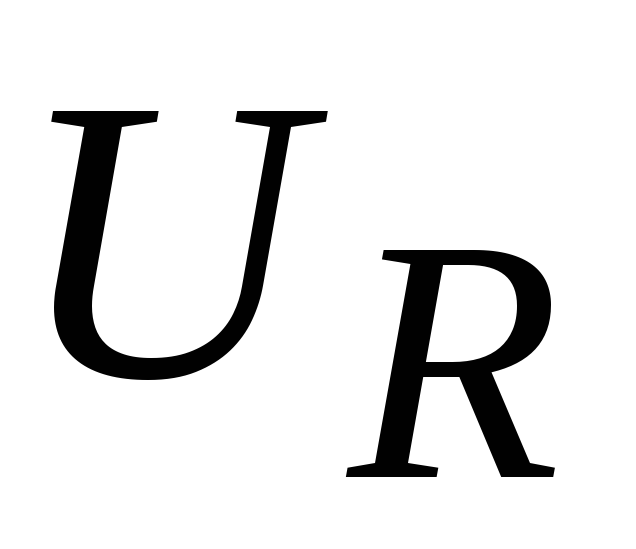итакой
цепочки.

Рассмотрим два
режима:

1. Дифференцирующая
   цепь –
   ,
   при этом возможны два варианта: а);
   б);

2. Разделительная
   цепь –
   ,
   при этом также: а);
   б);

а) б)

Рис.
1.11 — а) режим 1 –
,
б) режим 2 –.

1. Рассмотрим
   дифференцирующею цепочку под воздействием
   импульсной последовательности
   (рис.1.12).

Рис.
1.12 -Принципиальная схема укорачивающей
RC-цепочки

При импульсе
конденсатор Сзаряжается под
воздействием зарядного тока,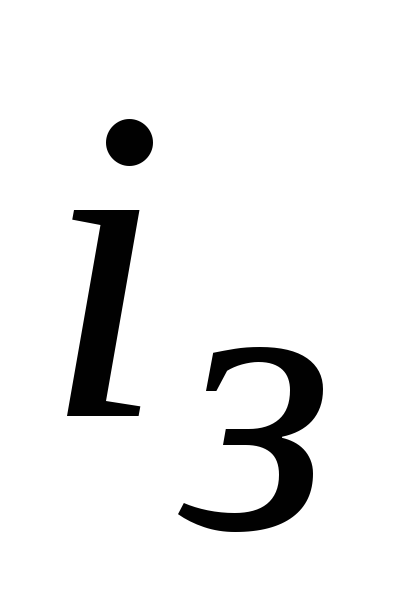
при паузе – разряжается, обуславливая
разрядный ток.
При этом.

Допустим
,тогда
им можно пренебречь ().

Рассмотрим режим
I, вариант а):,.

После окончания
импульса (момент времени
).

В период паузы ()
разряд конденсатораСполучается
полный, т.к.;

Рис.
1.13

;

.

Тогда

;

При
получим:

.

Значит получена
идеальная дифференцирующая цепь.
Следовательно для того чтобы цепь была
дифференцирующей необходимо выполнение
трёх условий:

1. ;

2. ;

3. ;

При этом график
напряжения
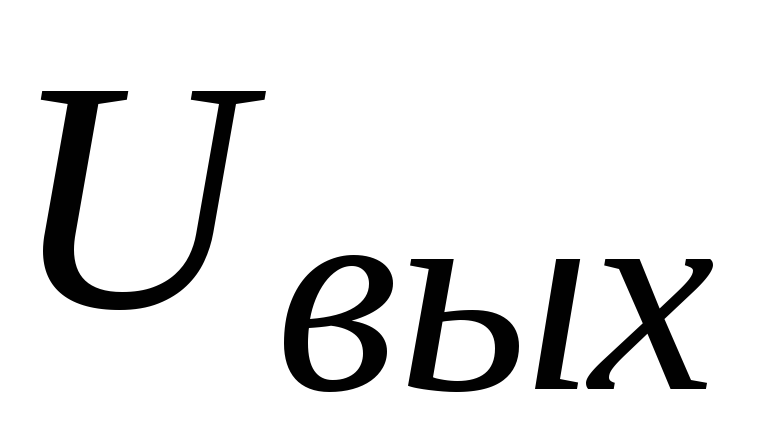при наличии импульсной последовательности
на входе будет иметь следующий вид
(рис.1.14):

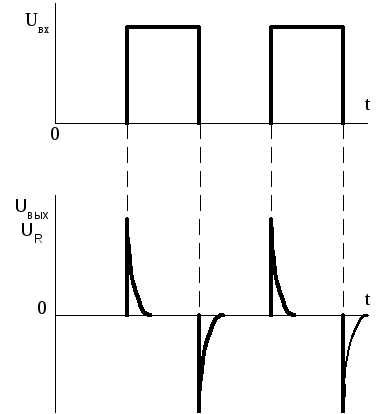
Рис.
1.14 — График напряжения
дифференцирующей цепи при наличии
импульсной последовательности на входе.

Режим I,
вариант б):,:

Графики напряжений
и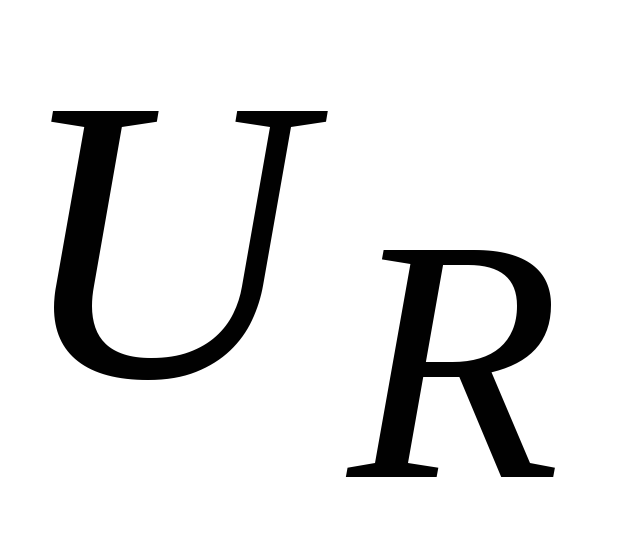приведены на рис.1.15. В этом режиме с
момента времени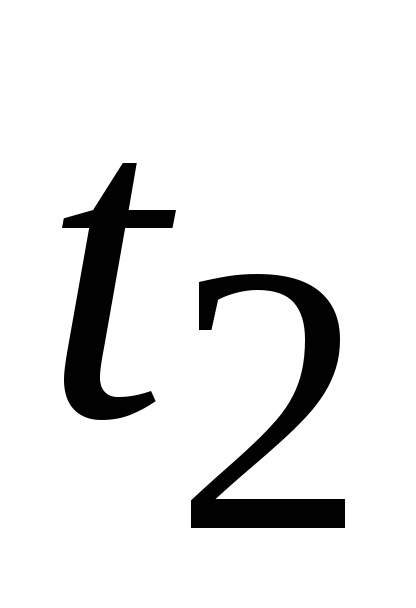имеют место, в отличие от варианта а),
новые начальные условия.
Такой режим называют режимом
негармонических возмущений.

В период импульса
переходные процессы аналогичны
рассмотренным в варианте а), а в период
паузы конденсатор Сне успевает
разрядиться до нуля за время,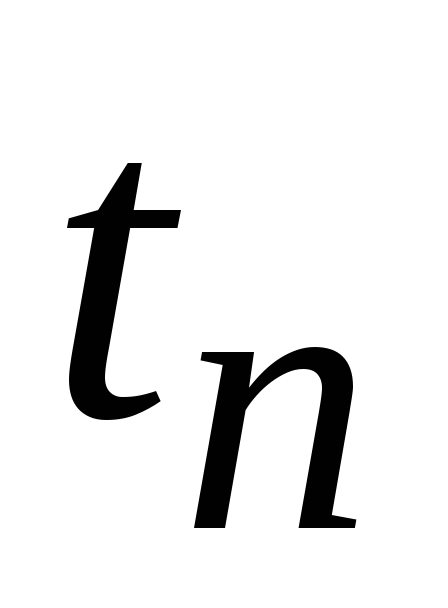
поэтому нулевые начальные условия не
выполняются и для дифференцирующей
цепочки такой вариант неприемлем.

Рис. 1.15

Режим IIпри,обеспечивает вариант разделительной
цепочки.

Вмомент времени,
после действия импульса, (см. рис.1.16),
а в момент времени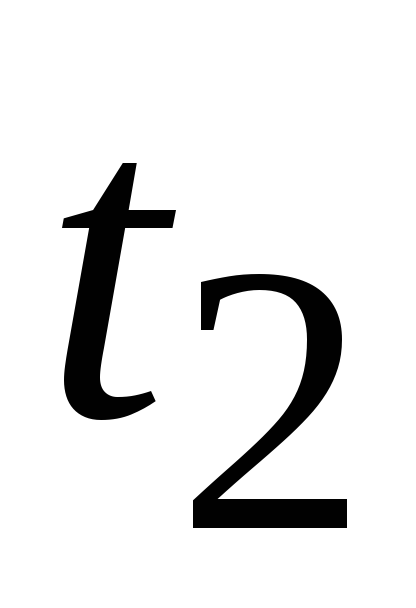имеют место нулевые начальные условия.
Сигнал на выходе повторяет сигнал на
входе. Следовательно, такая цепочка
является разделительной

Рис. 1.16

РежимII, при,,
аналогичен варианту б) режимаI,
поскольку в момент времени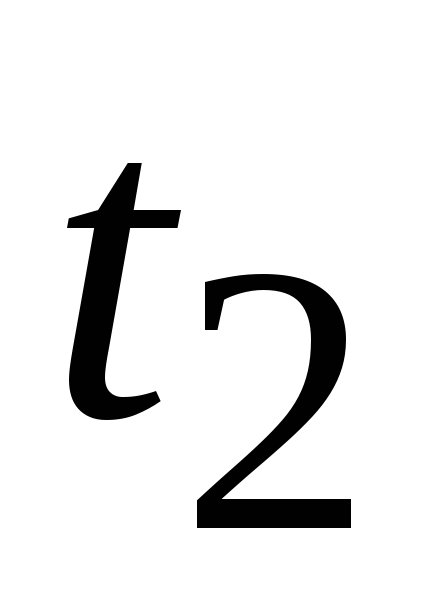также имеют место новые, ненулевые
начальные условия (рис.1.17) (режим
негармонических возмущений). Для
разделительной цепи такой вариант
неприемлем.

(б)

Рис. 1.17

Дифференцирующая RC-цепь.

Из названия цепи, в принципе, уже понятно, что за элементы входят в ее состав – это конденсатор и резистор И выглядит она следующим образом:

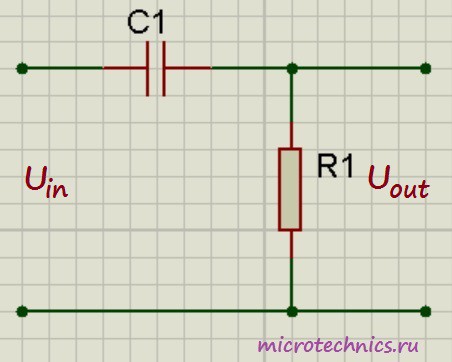
Работа данной схемы основана на том, что ток, протекающий через конденсатор, прямо пропорционален скорости изменения напряжения, приложенного к нему:

i = C\medspace\frac{dU_c}{dt}

Напряжения в цепи связаны следующим образом (по закону Кирхгофа):

u_{out} = u_{in}\medspace-\medspace u_c

В то же время, по закону Ома мы можем записать:

u_{out} = i R = C R\medspace\frac{dU_c}{dt}

Выразим u_c из первого выражения и подставим во второе:

u_{out} = C R\medspace\frac{dU_c}{dt} = C R\medspace(\frac{dU_{in}}{dt}\medspace-\medspace \frac{dU_{out}}{dt}\medspace)
u_{out} = C R\medspace\frac{dU_{in}}{dt}\medspace-\medspace C R\medspace\frac{dU_{out}}{dt}

При условии, что C R\medspace\frac{dU_{out}}{dt} << u_{out} (то есть скорость изменения напряжения низкая) мы получаем приближенную зависимость для напряжения на выходе:

u_{out} \approx C R\medspace\frac{dU_{in}}{dt}

Таким образом, цепь полностью оправдывает свое название, ведь напряжение на выходе представляет из себя дифференциал входного сигнала. Но возможен еще и другой случай, когда C R\medspace\frac{dU_{out}}{dt} >> u_{out} (быстрое изменение напряжения). При выполнении этого равенства мы получаем такую ситуацию:

C R\medspace\frac{dU_{in}}{dt} = C R\medspace\frac{dU_{out}}{dt}

То есть: U_{out} \approx U_{in}.

Можно заметить, что условие C R\medspace\frac{dU_{out}}{dt} << u_{out} будет лучше выполняться при небольших значениях произведения C R, которое называют постоянной времени цепи:

\tau = R C

Давайте разберемся, какой смысл несет в себе эта характеристика цепи Заряд и разряд конденсатора происходит по экспоненциальному закону:

u = U_0\medspace e^{-t/\tau}

Здесь U_0 – напряжение на заряженном конденсаторе в начальный момент времени. Теперь посмотрим, каким будет значение напряжения по истечении времени \tau:

U_{\tau} = U_0\medspace e^{-\tau/\tau} = U_0\medspace e^{-1} \approx 0.37\medspace U_0

Напряжение на конденсаторе уменьшится до 37% от первоначального. Таким образом, \tau – это время, за которое конденсатор:

• при заряде – зарядится до 63%
• при разряде – разрядится на 63% (разрядится до 37%)

С постоянной времени цепи мы разобрались, давайте вернемся к дифференцирующей RC-цепи. Теоретические аспекты функционирования мы разобрали, так что давайте посмотрим, как она работает на практике. А для этого попробуем подавать на вход какой-нибудь сигнал и посмотрим, что получится на выходе. В качестве примера, подадим на вход последовательность прямоугольных импульсов:

А вот как выглядит осциллограмма выходного сигнала (второй канал – синий цвет):

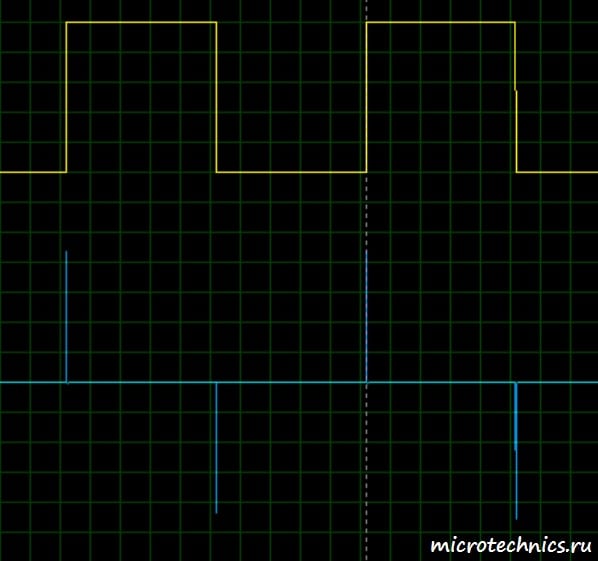
Что же мы тут видим?

Большую часть времени напряжение на входе неизменно, а значит его дифференциал равен 0 (производная константы = 0). Именно это мы и видим на графике, значит RC-цепь выполняет свою дифференцирующую функцию. А с чем же связаны всплески на выходной осциллограмме? Все просто – при “включении” входного сигнала происходит процесс зарядки конденсатора, то есть по цепи проходит ток зарядки и напряжение на выходе максимально. А затем по мере протекания процесса зарядки ток уменьшается по экспоненциальному закону до нулевого значения, а вместе с ним уменьшается напряжение на выходе, ведь оно равно U_{out} = i R. Давайте увеличим масштаб осциллограммы и тогда мы получим наглядную иллюстрацию процесса зарядки:

При “отключении” сигнала на входе дифференцирующей цепи происходит аналогичный переходный процесс, но только вызван он не зарядкой, а разрядкой конденсатора.

В данном случае постоянная времени цепи у нас имеет небольшую величину, поэтому цепь хорошо дифференцирует входной сигнал. По нашим теоретическим расчетам, чем больше мы будем увеличивать постоянную времени, тем больше выходной сигнал будет похож на входной. Давай проверим это на практике! Будем увеличивать сопротивление резистора, что и приведет к росту \tau:

Тут даже не надо ничего комментировать – результат налицо Мы подтвердили теоретические выкладки, проведя практические эксперименты, так что давайте переходить к следующему вопросу – к интергрирующим RC-цепям.

Синтез

Иногда требуется синтезировать RC-схему из заданной рациональной функции в s . Чтобы синтез пассивных элементов был возможен, функция должна быть положительно-действительной функцией . Для синтеза в виде RC-цепи все критические частоты ( полюса и нули ) должны быть на отрицательной действительной оси и чередоваться между полюсами и нулями с равным количеством каждого из них. Кроме того, критическая частота, ближайшая к началу координат, должна быть полюсом, если предположить, что рациональная функция представляет собой импеданс, а не полную проводимость.

Синтез может быть осуществлен с помощью модификации синтеза Фостера или синтеза Кауэра, используемого для синтеза цепей LC . В случае синтеза Кауэра получится лестничная сеть из резисторов и конденсаторов.

Дифференцирующие и интегрирующие RC — цепи

Рассмотренные выше случаи заряда и разряда конденсатора аналогичны ситуации в цепи, когда на вход RC
— цепи подается одиночный прямоугольный импульс длительностиtu
>>
t
.
Процессы, происходящие в такой электрической цепи (рис.13 а, б
) при подаче на вход ее в момент t
= 0
идеального прямоугольного импульса напряжения с амплитудой U
от генератора с внутренним сопротивлением R
2
= 0
, иллюстрируется временными диаграммами на рис.14.

http://pandia.ru/text/79/193/images/image018_17.gif» width=»265″ height=»182 src=»>

а

б

Р и с. 13

С моментаt
=
t
1
(положим t
1
= 0
), начинается процесс заряда конденсатора, описываемый уравнениями рис.14 а
, 14 б
).

При t
=
t
2
=
tu
напряжения на конденсаторе и резисторе описываются уравнениями(12), (14) и начинается разряд конденсаторов на сопротивление R
(рис.14 а
, 14 б
). При этом полярность напряжения на резисторе меняется на противоположную в соответствии с направлением тока разряда конденсатора (ф-ла 13). Следует заметить, что форма напряжения Uc
,
UR
существенно зависит от соотношения между постоянной времени цепи t
с
и длительностью импульса tu
=
t
2
—
t
1
. На рис. 14 представлены следующие соотношения между t
с
иtu
:

t
с
/ tu
= 1 ;
t
с
/ tu
>>
1;
t
с
/ tu
1.

В случае t
с
/ tu
>>
1
конденсатор за время действия импульса почти не заряжается и напряжение на резисторе R
практически повторяет по форме и амплитуде импульс на входе. В течение действия импульса в электрическом поле конденсатора накапливается незначительное количество энергии и поэтому после окончания действия импульса (t
=
t
2
)
в цепи практически не возникает переходный процесс. Такая RC
— цепь называется переходной (разделительной).

При t
=
tu
конденсатор успевает зарядиться до Uc
(t
с
/ tu
) = 0,63
U
,

UR
(t) = UR(t
с
) = 0,37U0.
После окончания действия импульса в цепи возникает переходный процесс, обусловленный рассеянием энергии, запасенной в конденсаторе. В цепи появляется разрядный ток, направление которого противоположно направлению зарядного тока. При

t
с
/ tu
1
конденсатор успевает зарядиться уже в начале импульса

(U0 = Uc).
На сопротивлении появится короткий импульс положительной полярности, обусловленный протеканием зарядного тока. В момент окончания входного импульса (t
=
t
2
)
в цепи возникает ток разряда конденсатора и на резисторе появится отрицательный импульс (рис.15 б
).

http://pandia.ru/text/79/193/images/image020_16.gif» width=»302″ height=»503 src=»>

а

б

Р и с. 14

Выходным элементом RC
—

цепи может быть как конденсатор С
(рис.15), так и резистор R
(рис.1 6).
Как следует из приведенных выше временных диаграмм Uc
(t
),
UR
(t
)
форма выходного сигнала будет зависеть от соотношения между длительностью импульсаtu
и постоянной времени t
с
.

http://pandia.ru/text/79/193/images/image022_11.gif» width=»294″ height=»617 src=»>

Р и с. 15 Р и с. 16

Рассмотрим цепь, изображенную на рис.15, т. е. с емкостным выходом:

UR
(t) = I(t)R = U
вх
(t) — Uc(t),
(26)

Uc
(t
) =
q
(t
) / С = 1/С
ò
I
(t
)
dt
= 1/С
ò
U
вх
(t
) —
Uc
(t
)
R
dt
,

еслиUc
(t
)
U
вх
(t
),
то Uc
(t
) = 1/С
ò
U
вх
(t
) ,
(27)

т. е. выходное напряжение пропорционально интегралу от входного. Поэтому RC
— цепь с емкостным выходом (t
с
/ tu
>>
1)
называется интегрирующей.

Рассмотрим RC
—

цепь, изображенную на рис. 16, т. е. с резистивным выходом:

I(t) = dq(t) / dt = C dUc(t) / dt

где q
(
t

)

— заряд на конденсаторе.

Напряжение на резисторе

UR
(t) = I(t)R = RC
×
dUc / dt = RC d/dt
×
U
вх
(t) — UR(t)
,

так как Uc
(t
) —
UR
(t
) =
U
вх
(t
).

Если UR(t) UR(t) = RC
×
dUвх(t) / dt,

т. е. выходное напряжение пропорционально производной входного. Такую RC
— цепь называют дифференцирующей (укорачивающей).
Обычно длительность выходных (укороченных) импульсов такой RC — цепи определяют на уровне 0,5
U
, т. е.

0,5 U0 = U0 e-tu/
t
c
,
(28)

Имеем: ln
0,5 = —
tu
t
,
илиtu
= 0,7
t
c
.

Выражение (28)
может быть использовано для экспериментального определения t
с
=
RC
.

Формирователи коротких импульсов (одновибраторы)

На
входы второй микросхемы поданы взаимно
инверсные сигналы со входа и выхода
первого инвертора, поэтому в тактическом
режиме сигнал на выходе устройства
всегда равен «1».
Сигнал «»
на выходе второй микросхемы появляется
только в том случае, когда сигнал на
входе первого инвертора переходит из
«»
в «1».
При этом пока происходит переключение
первого инвертора, на оба входа второй
микросхемы будет подан сигнал «1».
Длительность выходного импульса
формирователя можно увеличивать,
увеличивая время переключения первого
инвертора присоединением его к выходу
RC-цепи.

Когда
на входе «»,
емкость C
заряжается.

Когда
на вход подаем «1»,
емкость C
начинает разряжаться через открытый
выходной транзистор первого инвертора.
Пока емкость не разрядилась, на входе
второго инвертора две единицы и на
выходе формирователя «».

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Дифференцирующая RC цепь

Еще одно ругательное слово, которое пришло с математики – дифференцирующий. Башка начинает сразу же болеть от одного только их произношения. Но, куда деваться? Электроника и математика неразлучные друзья.

А вот и сама дифференциальная цепочка

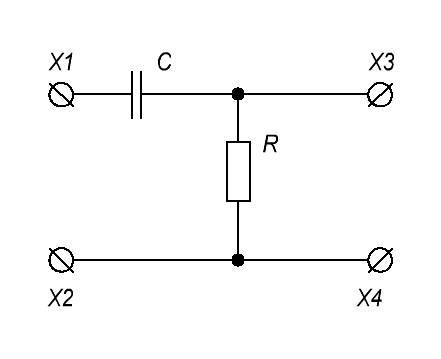
В схеме мы только переставили резистор и конденсатор местами

Ну а теперь проведем также все опыты, как мы делали с интегрирующей цепью. Для начала подаем на вход дифференциальной цепи низкочастотный двухполярный меандр с частотой в 1,5 Герца и с размахом в 5 Вольт.  Желтый сигнал – это сигнал с генератора частоты, красный –  с выхода дифференциальной цепочки:

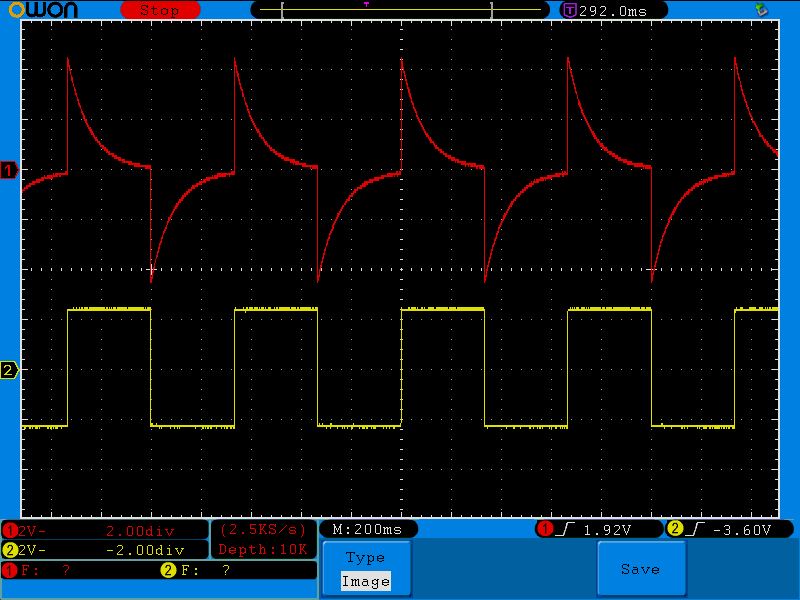
Как вы видите, конденсатор успевает почти полностью разрядится, поэтому у нас получилась вот такая красивая осциллограмма.

Давайте увеличим частоту до 10 Герц

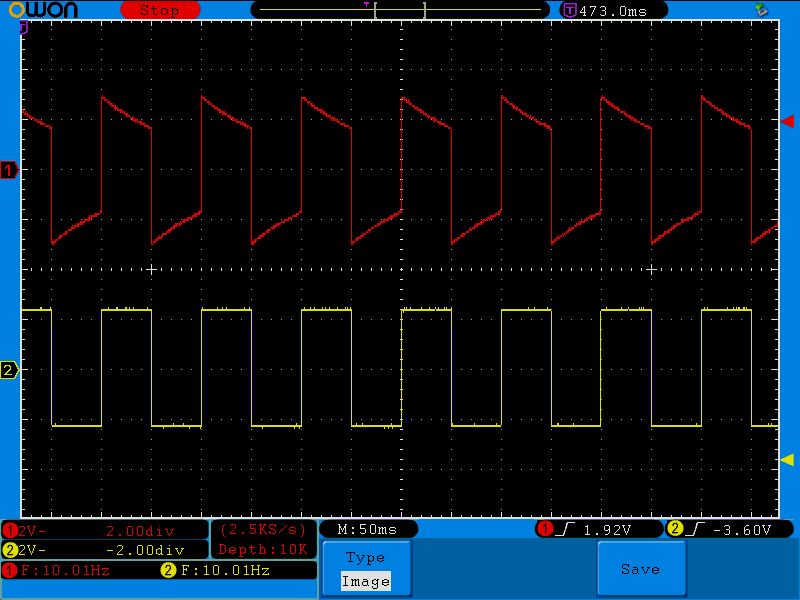
Как видите, конденсатор не успевает разрядиться, как уже приходит новый импульс.

Сигнал в 100 Герц сделал кривую разряда еще менее заметной.

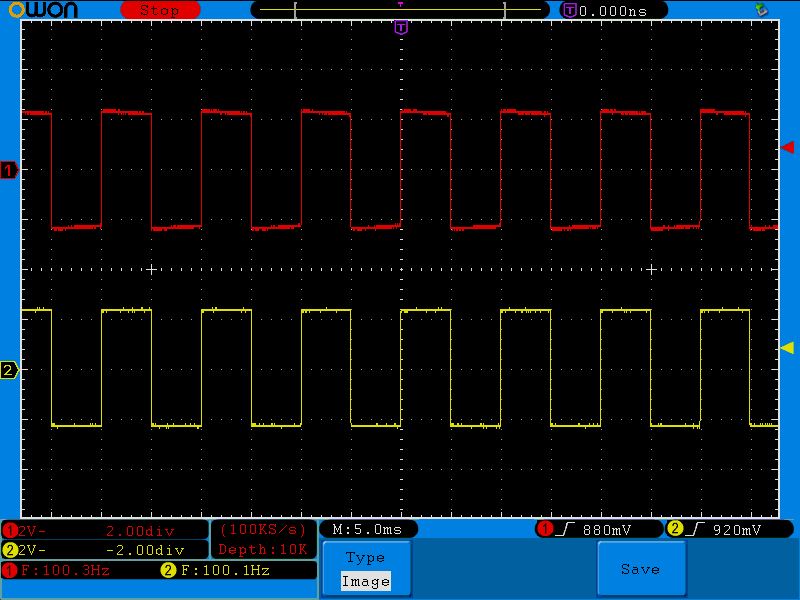
Ну и добавим частоту до 1 Килогерца

Какой на входе, такой и на выходе 😉 С такой частотой конденсатор вообще не успевает разряжаться, поэтому вершинки выходных импульсов гладкие и ровные.

Но и на этом тоже ништяки не заканчиваются.

Давайте я подниму входной сигнал над “уровнем моря”, то есть выведу его в положительную часть полностью. Смотрим, что получается на выходе (красный сигнал)

Ничего себе, красный сигнал по форме и по положению остался таким же, посмотрите – в нем нет постоянной составляющей, как в желтом сигнале, который мы подавали из нашего генератора функций.

Могу даже желтый сигнал вывести в отрицательную область, но на выходе мы все равно получим переменную составляющую сигнала без всяких хлопот:

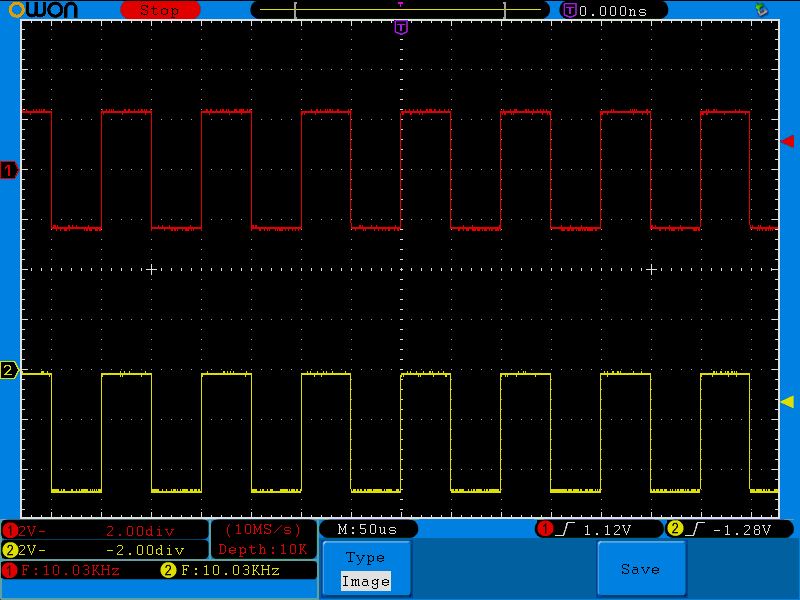
Да и вообще пусть сигнал будет с небольшой  отрицательной постоянной составляющей, все равно на выходе мы получим переменную составляющую:

Все то же самое касается и любых других сигналов:

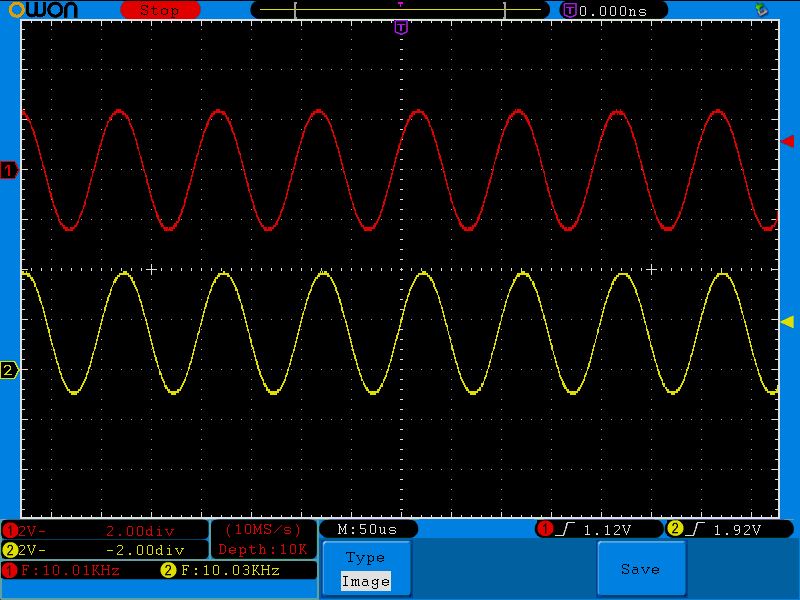
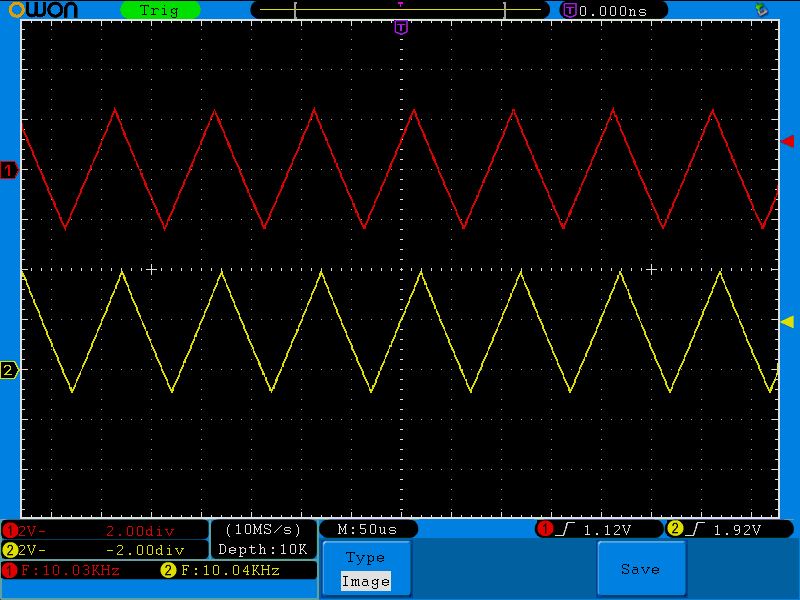
В результате опытов мы видим, что основная функция дифференциальной цепи – это выделение переменной составляющей из сигнала, который содержит в себе как переменную, так и постоянную составляющую. Иными словами – выделение переменного тока из сигнала, который состоит из суммы переменного тока и постоянного тока.

Почему так происходит? Давайте разберемся. Рассмотрим нашу дифференциальную цепь:

Если внимательно рассмотреть эту схему, то мы можем увидеть тот же самый делитель напряжения, как и в интегрирующей цепи. Конденсатор – частотно-зависимый радиоэлемент. Итак, если подать сигнал с частотой  в 0 Герц (постоянный ток), то у нас конденсатор тупо зарядится и потом вообще перестанет пропускать через себя ток. Цепь будет в обрыве. Но если мы будем подавать переменный ток, то и через конденсатор он тоже начнет проходить. Чем больше частота – тем меньше сопротивление конденсатора. Следовательно, весь переменный сигнал будет падать на резисторе, с которого мы как раз и снимаем сигнал.

Но если мы будем подавать смешанный сигнал, то есть переменный ток + постоянный ток, то на выходе мы получим просто переменный ток. В этом мы с вами уже убеждались на опыте. Почему так произошло? Да потому что конденсатор не пропускает через себя постоянный ток!

Резистивно-емкостные фильтры нижних частот

Пример двухкаскадного RC-фильтра нижних частот с неинвертирующим операционным усилителем с единичным коэффициентом передачи, который используется в качестве буфера между двумя каскадами фильтра

Фильтры нижних частот пропускают только низкочастотные сигналы и подавляют высокочастотные сигналы. Частота среза определяется компонентами фильтра.

Такие фильтры широко используются в электронике. Например, их используют в сабвуферах для того, чтобы не подавать на них звуки высоких частот, которые они не могут воспроизводить. Фильтры нижних частот используются также в радиопередатчиках для блокировки нежелательных высокочастотных составляющих в передаваемом сигнале. У тех, кто пользуется ADSL подключением к Интернету, всегда установлены частотные разделители с такими фильтрами нижних частот, которые предотвращают возникновение помех в аналоговых устройствах (телефонах) от сигналов DSL и воздействия помех от аналоговых устройств на оборудование DSL, подключенное к обычной телефонной линии.

Фильтры нижних частот используются для обработки сигналов перед их аналого-цифровым преобразованием. Такие фильтры улучшают качество аналоговых сигналов при их дискретизации и необходимы для подавления высокочастотных компонентов сигнала выше частоты Найквиста таким образом, чтобы он удовлетворял требованиям теоремы Котельникова для данной частоты дискретизации, то есть максимальная частота не должна быть выше половины частоты выборки.

На верхнем рисунке показан простой фильтр нижних частот. В нем используются только пассивные компоненты, поэтому он называется пассивным фильтром нижних частот (ФНЧ). В более сложных пассивных ФНЧ используются также катушки индуктивности.

В отличие от пассивных фильтров нижних частот, в активных фильтрах используются усилительные устройства, например, транзисторы или операционные усилители. В пассивные фильтрах также часто имеются операционные усилители, применяемые для развязки. В зависимости от количества конденсаторов и катушек индуктивности, влияющих на крутизну частотной характеристики фильтра, они обычно называются «фильтрами первого порядка», «второго порядка» и так далее. Фильтр, состоящий только из одного резистора и одного конденсатора, называется фильтром первого порядка.

Простой пассивный RC-фильтр верхних частот