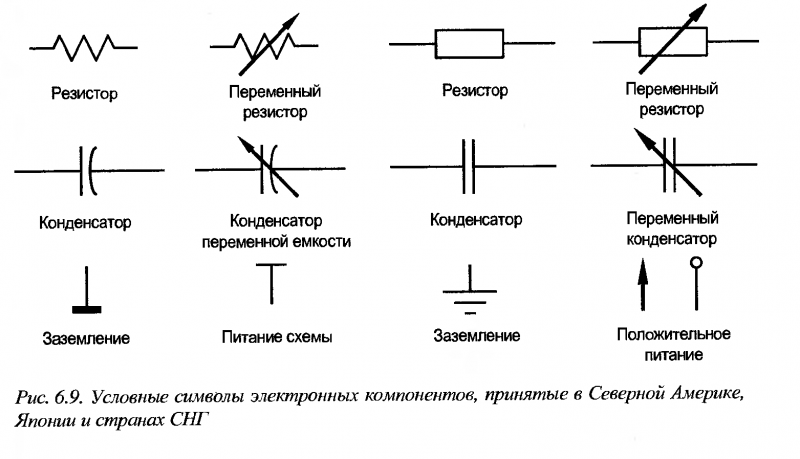
Построение таблицы истинности. сднф. скнф. полином жегалкина

3.7. Что такое сумматор

Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел.

Сумматор служит, прежде всего, центральным узлом арифметико-логического
устройства компьютера, однако он находит применение также и в других устройствах
машины.

Многоразрядный двоичный сумматор, предназначенный для сложения
многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных
сумматоров, с рассмотрения которых мы и начнём. Условное обозначение
одноразрядного сумматора на рис. 3.8.

Рис. 3.8.

При сложении чисел A и B в одном i-ом разряде приходится иметь дело с
тремя цифрами:

1. цифра a_i первого
слагаемого;

2. цифра b_i второго
слагаемого;

3. перенос p_i–1 из младшего
разряда.

В результате сложения получаются две цифры:

1. цифра c_i для суммы;

2. перенос p_i из данного
разряда в старший.

Таким образом, одноразрядный двоичный сумматор есть устройство с тремя
входами и двумя выходами, работа которого может быть описана следующей
таблицей истинности:

Входы	Выходы
Первое слагаемое	Второе слагаемое	Перенос	Сумма	Перенос
1	1
1	1
1	1	1
1	1
1	1	1
1	1	1
1	1	1	1	1

Если требуется складывать двоичные слова длиной два и более бит, то можно
использовать последовательное соединение таких сумматоров, причём для двух
соседних сумматоров выход переноса одного сумматора является входом для
другого.

Например, схема вычисления суммы C = (с₃ c₂
c₁ c) двух двоичных трехразрядных чисел A =
(a₂ a₁ a) и B = (b₂ b₁
b) может иметь вид:

Основные направления прикладного использования логики в информатике

1. написание компьютерных программ и их верификация.
2. при проектировании вычислительных устройств используется как теоретический инструмент.
3. Использование логических операций в электронных микросхемах в качестве базовых.
4. логический подход к представлению и решению различных практических задач с использованием вычислительной техники.

Определение 2

Стандартное математическое представление любого вычисления − это отображение переменных (их внутреннего состояния) вычислительного устройства на входе в новое состояние на выходе. В алгебре логики решается стандартная задача, а именно: определяется функциональная полнота логических связок, то есть проверяется, является ли фиксированный набор логических операций достаточным для того, чтобы представить новое результирующее значение путём комбинации любых других (базовых) функций. А это значит, что базовые логические устройства должны быть универсальными и позволять решать большое число задач.

Работу большинства вычислительных устройств, которые существуют в настоящее время, прекрасно описывает алгебра логики, разработанная Джорджем Булем. К таким устройствам относятся триггеры, сумматоры, группы переключателей, Кроме того булева алгебра и компьютеры связаны между собой при помощи используемой в ЭВМ двоичной системы счисления. Поэтому в устройствах компьютера можно хранить и преобразовывать и значения логических переменных, и числа.

Определение 3

Логические элементы — это электронные устройства, которые по определенному закону преобразуют проходящие через них двоичные электрические сигналы.

Логические элементы имеют один (инвертор) или несколько входов, на которые подаются электрические сигналы, обозначаемые условно $0$, если сигнал отсутствует, и $1$, если электрический сигнал имеется. Выход у логических элементов один, откуда снимается новый, преобразованный электрический сигнал.

Все электронные схемы компьютера могут быть реализованы с помощью трёх базовых логических элементов И, ИЛИ, НЕ.

Логический элемент НЕ (инвертор). Простейший логический элемент, реализующий функцию отрицания (инверсию). Унарный элемент – элемент, у которого один вход и один выход.

На функциональных схемах обозначается

Рисунок 1.

Если на вход инвертора подаётся $1$, то на выходе реализуется $0$ и наоборот.

Логический элемент И (конъюнктор) реализует умножение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:

Рисунок 2.

Если на входе конъюнктора все входные сигналы имеют значение $1$, то на выходе тоже будет сигнал $1$, в противном случае на выходе будет сигнал $0$.

Логический элемент ИЛИ (дизъюнктор) реализует сложение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:

Рисунок 3.

Если на вход дизъюнктора поступает хотя бы один сигнал равный $1$, то выходе тоже будет сигнал $1$.

Роль базовых логических элементов в создании схем играют ещё два логических элемента: И-НЕ и ИЛИ-НЕ.

Логический элемент И-НЕ (отрицание конъюнкции) выполняет логическую функцию штрих Шеффера. Операция бинарная, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается следующим образом:

Рисунок 4.

Логический элемент ИЛИ-НЕ (отрицание дизъюнкции) выполняет логическую функцию стрелка Пирса. Тоже бинарная операция, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается так:

Рисунок 5.

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Моделирование функциональных схем

Синхронные бинарные модели дают возможность проверки выполнения логическими схемами требуемых логических функций, не учитывая запаздывание сигналов в компонентах и возможность сбоев в работе. Построение синхронных моделей логических схем осуществляется способами решения системы логических уравнений, к которым можно отнести способ простой итерации и методику Зейделя.

Способ простой итерации заключается в том, что выражение $f(x) = 0$ можно заменить, используя равносильные преобразования, выражением типа $x = j(x)$, а далее необходимо выстроить последовательные приближения $X_0, X_1, …, X_k$ к корню уравнения $x^*$ согласно закона $X_k + 1 = Ω (X_k) k = 0, 1, 2, …$, где $k$ является номером итерации. Корень уравнения находится с некоторой допустимой погрешностью $│X_k — x^*│≤ ε│X_0 — x^*│$, где $x^*$ является точным решением.

Рисунок 1. Схема. Автор24 — интернет-биржа студенческих работ

Для приведённой на рисунке один схемы математическую модель можно представить в виде следующего набора уравнений логики:

Рисунок 2. Набор уравнений. Автор24 — интернет-биржа студенческих работ

Входные сигналы изменяются в таком порядке:

a: 0-0, b: 1-0, c: 1-1, d: 0-1.

В таблице ниже отображено решение способом простой итерации:

Рисунок 3. Таблица. Автор24 — интернет-биржа студенческих работ

Процесс итерации останавливается, если пара, следующих один за другим сигнальных наборов, станут одинаковыми. По этой методике в уравнения следует подставлять величины, которые получились после предыдущей итерации.

При использовании методики Зейделя в уравнения следует подставить величины текущей итерации. Ниже приведена таблица с решением по этому методу.

Рисунок 4. Таблица. Автор24 — интернет-биржа студенческих работ

Следует заметить, что при этой методике количество итераций уменьшилось до четырёх шагов. Для дальнейшего повышения эффективности решения применяется начальное ранжирование модельных уравнений. Процесс ранжирования состоит в назначении каждому элементу и переменой модели величин рангов, которые должны соответствовать следующим нормам:

1. Необходимо разорвать на схеме все линии обратной связи, что вызовет появление добавочных входных линий (псевдо входов).
2. Каждой входной переменной, включая псевдо входы, присваивается ранг, равный нулю.
3. Каждому элементу и его переменным на входах присваивается ранг k, когда элемент имеет все проранжированные входы, а старший из рангов равняется k-1.

Согласно этому правилу для схемы, представленной на рисунке один, проранжированный набор уравнений, следующий:

Рисунок 5. Набор уравнений. Автор24 — интернет-биржа студенческих работ

В таблице ниже приведено решение по методике Зейделя.

Рисунок 6. Таблица. Автор24 — интернет-биржа студенческих работ

Отмечаем сокращение количества итераций до двух.

Основанием событийного моделирования является анализ процессов лишь для элементов, у которых меняются значения входных сигналов. Статистика функционирования цифровых устройств может показать, что активными в каждый текущий момент времени являются только от одного до десяти процентов всего логического набора элементов. По этой причине событийное моделирование имеет повышенное быстродействие в сравнении со сквозным. Самым распространённым является алгоритм асинхронного событийного моделирования, который объединяет лучшие качества асинхронного и событийного моделирований.

Следующим шагом анализа считается выполнение проверки работы модуля при учёте задержек в каждом элементе, определяющем общую структуру, и влиянии разнообразных мешающих воздействий. Такой анализ позволяет определить критический уровень сигналов и возникновение иных сбойных ситуаций. Возникшее небольшое рассогласование на входных контактах компонента способно вызвать неверный выходной сигнал. Возбудителями рассогласования могут стать сигналы синусоидальной, трапецеидальной, экспоненциальной формы на входах логических элементов, временные запаздывания в элементах и каналах передачи сигналов.

Понятие многозначности можно трактовать по-разному:

1. Трактовка многозначности по типу изменения сигналов логики.
2. Трактовка многозначности в смысле квантования сигналов логики по их уровням.

Первый вид включает в себя способы многозначной логики, которые основаны на применении помимо величин нуль и единица, принятых в алгебре Буля, разных отображений сигналов событий.

Вторым видом многозначности является квантование сигналов по уровням, то есть учитываются промежуточные состояния между двумя основными, логическим нулём и логической единицей.

Начало работы

Первым делом необходимо составить таблицу истинности по формуле

где N – количество возможных вариантов, а i – количество выходных сигналов.

В представленном случае это будет выглядеть так:

На основе полученных данных можно перейти к построению таблицы истинности. Для наглядности входные сигналы были обозначены как A, B, C и D, выходной как F.

После построения таблицы истинности можно приступать к получению СДНФ. Это выполняется в два шага:

1. Выделяются строчки таблицы истинности, в которых F=1.
2. Выписывается конъюнкция переменных у всех выделенных строк по следующей формуле: если значение переменной равно 1, то в конъюнкцию включается сама переменная. Если значение равно 0, то включается отрицание переменной. Полученные конъюнкции нужно связать в дизъюнкцию.

По итогу выходит такая СДНФ:

2. Создание карты Карно, минимизация и приведение к базису И-НЕ

Полученную СДНФ необходимо сократить при помощи карт Карно.

Три шага для построения карт Карно:

1. так как используются четыре переменные (A, B, C и D), то строится таблица 5×5 клеток;
2. таблица заполняется на основе «координат» из таблицы истинности (из строк, в которых F=1) или СДНФ (суть одна. Просто кому как удобнее);
3. в заключение смежные клетки объединяются в группы. Группы не должны содержать нули. Группы должны быть кратны двум. Группы могут пересекаться.

В итоге получилось 4 группы:

Следующее действие — минимизация полученных групп. Общий принцип можно свести к следующему: Если 11 — значение не меняется; Если 00 — присваивается отрицание; Если 01 (или 10) — вычеркивается.

Полученные произведения связываются в дизъюнкцию:

После чего составленное выражение приводится к базису И-НЕ при помощи закона де Моргана (отрицание конъюнкции есть дизъюнкция отрицаний, отрицание дизъюнкции есть конъюнкция отрицаний):

Обратите внимание на изменения — появилось двойное отрицание (по одной на «группу» и одно общее) и изменились знаки. По желанию также можно составить логическую схему

Почему по желанию? Потому что дальше будет составление электронной схемы на основе логических элементов, а она, по своей сути, является той же самой логической схемой, но с возможностью проверки работоспособности

По желанию также можно составить логическую схему. Почему по желанию? Потому что дальше будет составление электронной схемы на основе логических элементов, а она, по своей сути, является той же самой логической схемой, но с возможностью проверки работоспособности.

Пример логической схемы:

3. Электронная схема на основе логических элементов

Основные расчеты завершены. Теперь можно отложить листок с ручкой и линейкой. Переходим в Electronics Workbench.

В данном случае этот этап выступает «промежуточным» и упрощает процесс перехода от выражения в базисе И-НЕ к электронной схеме на основе микросхем.

1 — Питание; 2 — Переключатели, используемые для подачи сигналов; 3 — Индикаторы (применяются для наглядной проверки работоспособности); 4 — Логические элементы типа «НЕ»; 5 — Логические элементы типа «3И-НЕ»; 6 — Логический элемент типа «4И-НЕ»; 7 — Заземление.

Как можно заметить, логические элементы электронной схемы внешне отличаются от тех, что были представлены ранее (в логической схеме). Это связано с тем, что в Electronics Workbench условное графическое обозначение логических элементов выполнено по стандартам ANSI, тогда как показанная ранее логическая схема была выполнена в соответствии ГОСТ 2.743-91.

Работоспособность электронной схемы проверяется по таблице истинности. Для этого нужно нажать кнопку запуска

и начать производить переключения, проводя сравнение с таблицей истинности.

ВАЖНО: нужно проверять каждую строчку. Выборочная проверка ничего не даст

4. Электронная схема на основе микросхем

На базе имеющихся данных производится построение электронной схемы на основе микросхем (также по полученной схеме можно будет ориентироваться во время проектирования печатной платы).

Как можно заметить, в полученной электронной схеме использовано 4 микросхемы — 7404 (аналог К155ЛН1), 7410 (аналог К155ЛА4), 7410 (аналог К155ЛА4) и 7420 (аналог К155ЛА1). Для того чтобы понять, как происходит подключение, следует обратиться к фактическому изображению микросхем.

Сначала это может показаться сложным, но со временем вы поймете, что это не так уж и трудно

ВАЖНО: не забывайте делать проверку

By :

Логические основы работы компьютера

Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.

Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.

Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».

Логический элемент «НЕ» (инвертор)

Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.

У этого элемента один вход и один выход. На функциональных схемах он обозначается:

Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.

Проверь соответствие логического элемента «НЕ» логическому элементу «НЕ». Воспользуйся тренажером Логические элементы.xlsx

Логический элемент «И» (конъюнктор)

Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.

Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:

Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.

Проверь соответствие логического элемента «И» логическому элементу «И».  Воспользуйся тренажером Логические элементы.xlsx

Логический элемент «ИЛИ» (дизъюнктор)

Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:

Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.

На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.

Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.

Проверь соответствие логического элемента «ИЛИ» логическому элементу «ИЛИ».  Воспользуйся тренажером Логические элементы.xlsx

Пример 1.Составьте логическую схему для логического выражения: F=A \/ B /\ A.

1.Две переменные – А и В.

2.Две логические операции: 1-/\, 2-\/.

3.Строим схему:

Пример 2.Постройте логическую схему, соответствующую логическому выражению F=А/\В\/ ¬(В\/А). Вычислить значения выражения для А=1,В=0.

1.Переменных две: А и В; 1 4 3 2

2.Логических операций три: /\ и две \/; А/\В\/ ¬ (В\/ А).

3.Схему строим слева направо в соответствии с порядком логических операций:

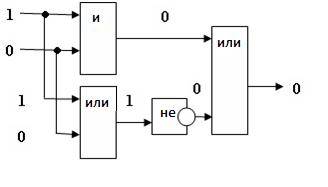
4.  Вычислим значение выражения: F=1 /\ 0 \/ ¬(0 \/ 1)=0

3.11. Что такое переключательная схема

В компьютерах и других автоматических устройствах широко применяются
электрические схемы, содержащие сотни и тысячи переключательных элементов: реле,
выключателей и т.п. Разработка таких схем весьма трудоёмкое дело. Оказалось, что
здесь с успехом может быть использован аппарат алгебры логики.

Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и
разомкнутое. Переключателю Х поставим в соответствие логическую
переменную х, которая принимает значение 1 в том и только в том случае,
когда переключатель Х замкнут и схема проводит ток; если же переключатель
разомкнут, то х равен нулю.

Будем считать, что два переключателя Х и связаны
таким образом, что когда Х замкнут, то
разомкнут, и наоборот. Следовательно, если переключателю Х поставлена в
соответствие логическая переменная х, то переключателю должна
соответствовать переменная .

Всей переключательной схеме также можно поставить в соответствие логическую
переменную, равную единице, если схема проводит ток, и равную нулю — если не
проводит. Эта переменная является функцией от переменных, соответствующих всем
переключателям схемы, и называется функцией проводимости.

Найдем функции проводимости F некоторых переключательных схем:

a)  

Схема не содержит переключателей и проводит ток всегда, следовательно
F=1; 

б)  

Схема содержит один постоянно разомкнутый контакт, следовательно
F=0; 

в)  

Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х
разомкнут, следовательно, F(x) = x; 

г)  

Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда
х замкнут, следовательно, F(x) = ; 

д)  

Схема проводит ток, когда оба переключателя замкнуты, следовательно,
F(x) = x . y; 

е)  

Схема проводит ток, когда хотя бы один из переключателей замкнут,
следовательно, F(x)=x v y; 

ж)  

Схема состоит из двух параллельных ветвей и описывается функцией . 

Две схемы называются равносильными, если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале). Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей.

Задача нахождения среди равносильных схем наиболее простых является очень
важной. Большой вклад в ее решение внесли российские учёные Ю.И

Журавлев,
С.В. Яблонский и др.

При рассмотрении переключательных схем возникают две основные задачи:
синтез и анализ схемы.

СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трём
этапам:

1. составлению функции проводимости по таблице истинности, отражающей эти
   условия;
2. упрощению этой функции;
3. построению соответствующей схемы.

АНАЛИЗ СХЕМЫ сводится к

1. определению значений её функции проводимости при всех возможных наборах
   входящих в эту функцию переменных.
2. получению упрощённой формулы.

Примеры.

1. Построим схему, содержащую 4 переключателя
x, y, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут
контакт переключателя t и какой-нибудь из остальных трёх контактов.

Решение. В этом случае можно обойтись без построения таблицы
истинности. Очевидно, что функция проводимости имеет вид F(x, y, z, t) =
t . (x v y v z), а схема выглядит так:

2. Построим схему с пятью переключателями,
которая проводит ток в том и только в том случае, когда замкнуты ровно четыре из
этих переключателей.

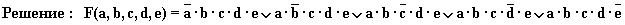
Схема имеет вид:

3. Найдем функцию проводимости схемы:

Решение. Имеется четыре возможных пути прохождения тока при замкнутых
переключателях a, b, c, d, e : через переключатели a, b; через переключатели a,
e, d; через переключатели c, d и через переключатели c, e, b. Функция
проводимости F(a, b, c, d, e) = a . b   v   a .
e . d   v   c . d   v   c .
e . b.

4. Упростим переключательные схемы:

а)  

Решение:   

Упрощенная схема:

б)  

.

Здесь первое логическое слагаемое является
отрицанием второго логического слагаемого , а
дизъюнкция переменной с ее инверсией равна 1.

Упрощенная схема :

в)  

Упрощенная схема:

г)  

Упрощенная схема:

д)  

(по
закону склеивания)

Упрощенная схема:

е)  

Решение:

Упрощенная схема:

Материалы по MMLogic

К сожалению, материалов по MMLogic на русском языке очень мало:

• Презентации В.И. Глезденева
  (МБОУ Лицей № 8, г. Сосновый Бор).
• Разработка уроков Н.А. Пасечник
  на портале «Сеть творческих учителей».

Материалов на английском немногим больше:

• Сайт компании Softronix (www.softronix.com)
• Проекты Джеймса Ларсона (www.dst-corp.com)
• Введение в MMLogic (университет Кэмбриджа, www.cl.cam.ac.uk)
• Лабораторная работа по схемотехнике
  (университет Виттенберг, www4.wittenberg.edu)
• Лабораторная работа
  «Введение в логику« (Калифорнийский университет, classes.soe.ucsc.edu)
• Видео: Урок 1: простые цепи (www.youtube.com)
• Видео: Урок 2: элементы И и ИЛИ (www.youtube.com)
• Видео: Урок 3-1: генератор таблиц истинности (www.youtube.com)
• Видео: Урок 3-2: генератор таблиц истинности (www.youtube.com)
• Видео: Урок 3-3: генератор таблиц истинности (www.youtube.com)
• Видео: Полный сумматор в MMLogic (www.youtube.com)
• Видео: Приёмник и передатчик сигналов в MMLogic (www.youtube.com)
• Видео: Использование Робота (www.youtube.com)

Что это такое?

Multimedia Logic (MMLogic) — это
бесплатная программа-конструктор, с помощью которой можно моделировать логические схемы любой сложности и
устройства компьютера. Её автор — George Mills —
разместил на сайте фирмы Softronix не только
исполняемый файл программы, но и её исходные тексты на Visual C++ 7.1.

В оригинальной версии MMLogic существует две проблемы:

1. интерфейс программы — англоязычный;
2. в программе используются зарубежные обозначения логических элементов,
   которые сильно отличаются от отечественных (ГОСТ 2.743—91).

Эти проблемы существенно сдерживали внедрение программы MMLogic в
учебный процесс в российских школах. На этой странице представлена
русскоязычная версия программы, в которой используются обозначения
логических элементов согласно ГОСТ 2.743—91.

Спасибо В.И. Глезденеву (МБОУ Лицей № 8, г. Сосновый Бор), который
привлёк внимание автора к этой программе.