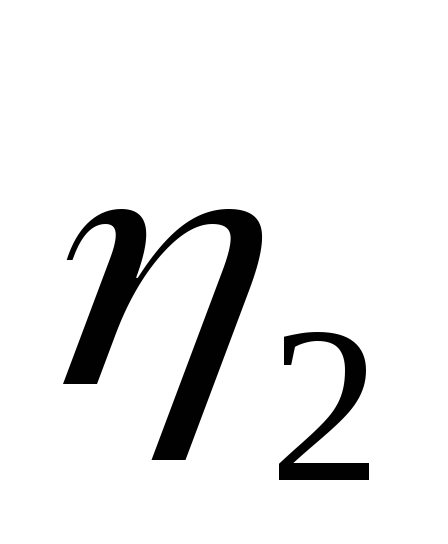Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в excel

Характерные значения и стандарты

Объект	Тип напряжения	Значение (на вводе потребителя)	Значение (на выходе источника)
Электрокардиограмма	Импульсное	1-2 мВ	—
Телевизионная антенна	Переменное высокочастотное	1-100 мВ	—
Гальванический цинковый элемент типа АА («пальчиковый»)	Постоянное	1,5 В	—
Литиевый гальванический элемент	Постоянное	3 В — 3,5 В (в исполнении пальчикового элемента, на примере Varta Professional Lithium, AA)	—
Логические сигналы компьютерных компонентов	Импульсное	3,5 В; 5 В	—
Батарейка типа 6F22 («Крона»)	Постоянное	9 В	—
Силовое питание компьютерных компонентов	Постоянное	5 В, 12 В	—
Электрооборудование автомобилей	Постоянное	12/24 В	—
Блок питания ноутбука и жидкокристаллических мониторов	Постоянное	19 В	—
Сеть «безопасного» пониженного напряжения для работы в опасных условиях	Переменное	36—42 В	—
Напряжение наиболее стабильного горения свечи Яблочкова	Постоянное	55 В	—
Напряжение в телефонной линии (при опущенной трубке)	Постоянное	60 В	—
Напряжение в электросети Японии	Переменное трёхфазное	100/172 В	—
Напряжение в домашних электросетях США	Переменное трёхфазное	120 В / 240 В (сплит-фаза)	—
Напряжение в бытовых электросетях России	Переменное трёхфазное	220/380 В	230/400 В
Разряд электрического ската	Постоянное	до 200—250 В	—
Контактная сеть трамвая и троллейбуса	Постоянное	550 В	600 В
Разряд электрического угря	Постоянное	до 650 В	—
Контактная сеть метрополитена	Постоянное	750 В	825 В
Контактная сеть электрифицированной железной дороги (Россия, постоянный ток)	Постоянное	3 кВ	3,3 кВ
Распределительная воздушная линия электропередачи небольшой мощности	Переменное трёхфазное	6—20 кВ	6,6—22 кВ
Генераторы электростанций, мощные электродвигатели	Переменное трёхфазное	10—35 кВ	—
На аноде кинескопа	Постоянное	7—30 кВ	—
Статическое электричество	Постоянное	1—100 кВ	—
На свече зажигания автомобиля	Импульсное	10—25 кВ	—
Контактная сеть электрифицированной железной дороги (Россия, переменный ток)	Переменное	25 кВ	27,5 кВ
Пробой воздуха на расстоянии 1 см		10—20 кВ	—
Катушка Румкорфа	Импульсное	до 50 кВ	—
Пробой слоя трансформаторного масла толщиной 1 см		100—200 кВ	—
Воздушная линия электропередачи большой мощности	Переменное трёхфазное	35 кВ, 110 кВ, 220 кВ, 330 кВ	38 кВ, 120 кВ, 240 кВ, 360 кВ
Электрофорная машина	Постоянное	50—500 кВ	—
Воздушная линия электропередачи сверхвысокого напряжения (межсистемные)	Переменное трёхфазное	500 кВ, 750 кВ, 1150 кВ	545 кВ, 800 кВ, 1250 кВ
Трансформатор Тесла	Импульсное высокочастотное	до нескольких МВ	—
Генератор Ван де Граафа	Постоянное	до 7 МВ	—
Грозовое облако	Постоянное	От 2 до 10 ГВ	—

Формула, примеры решения задач

Для четырех измеренных значений величины b формула среднеквадратичного отклонения будет выглядеть следующим образом:

\(\sigma=\sqrt{\frac{\triangle b_1+\triangle b_2+\triangle b_3+\triangle b_4}4}\)

где Db₁ — Db₄ являются абсолютными погрешностями каждой исследуемой величины.

Рассмотрим пример решения конкретной задачи.

Задача

При проведении лабораторной работы по физике школьники несколько раз измерили напряжение электрического тока и получили следующие значения:

\(U_1=4.22B\\U_2=4.30B\\U_3=4.27B\\U_4=4.23B\\U_5=4.20B\)

Необходимо рассчитать погрешности (абсолютные и относительные) каждого измерения, дисперсию и среднеквадратическое отклонение.

Решение

Определим среднее арифметическое значение напряжения в данной работе:

\(U_c=\sqrt{\frac{U_1+U_2+U_3+U_4+U_5}5}=\frac{4.22+4.30+4.27+4.23+4.20}5=4.244B\)

Теперь рассчитаем для каждого полученного измерения абсолютную и относительную погрешности. Так как абсолютная погрешность определяется как разница между средним арифметическим и полученным значением, то

\(\triangle U_1=0.024\\\triangle U_2=-0.056\\\triangle U_3=-0.026\\\triangle U_4=0.014\\\triangle U_5=0.044\)

Находим относительную погрешность:

\(\sigma_1=\frac{\left|U_1\right|}{U_c}\times100\%=0.50\%\\\sigma_2=\frac{\left|U_2\right|}{U_c}\times100\%=1.06\%\\\sigma_3=\frac{\left|U_3\right|}{U_c}\times100\%=0.50\%\\\sigma_4=\frac{\left|U_4\right|}{U_c}\times100\%=0.25\%\\\sigma_5=\frac{\left|U_5\right|}{U_c}\times100\%=0.84\%\\\)

Зная абсолютные погрешности несложно вычислить дисперсию:

\(D=\frac{\triangle U_1^2+{\triangle U_2}^2+{\triangle U_3}^2+{\triangle U_4}^2+{\triangle U_5}^2}5=0.001304\\\)

Теперь можно вычислить среднеквадратичное отклонение:

Подытожим

RMS и пиковая мощность играют важную роль в вашей аудио системе,
и они жизненно важны при сравнении ваших колонок с усилителями или сабвуферами. При согласовании колонок или сабвуферов с усилителями следует сравнить либо их значения RMS, либо их пиковые значения.

Поэтому не следует путаться при сравнении пиковых и среднеквадратичных значений. Это обеспечит максимальную отдачу от каждого компонента. Если выходные значения мощности устройств не соответствуют друг другу, компоненты могут перегреться и создать уже другие проблемы

Тем не менее, важно подчеркнуть, что вы всегда должны использовать среднеквадратичные значения, а не пиковую мощность, при сравнении  и выборе оборудования

В некоторых интернет магазинах тип мощности колонок и ее значение не указаны. В таком случае лучше посмотреть значения максимальной (пиковой) и среднеквадратичной мощностей на официальном сайте производителя.

Небольшой обзор топ колонок 2019 года:

В обычных формах волны

Синусоидальная , квадратная , треугольная и пилообразная формы сигналов.

Прямоугольная импульсная волна с коэффициентом заполнения D, соотношением длительности импульса ( ) и периода (T); показано здесь с a = 1.τ{\ Displaystyle \ тау}

График зависимости напряжения синусоидальной волны от времени (в градусах), показывающий среднеквадратичное, пиковое (PK) и размах напряжения (PP).

Если форма волны представляет собой чистую синусоидальную волну , отношения между амплитудами (размахом, пиком) и среднеквадратичным значением фиксированы и известны, как и для любой непрерывной периодической волны. Однако это неверно для сигнала произвольной формы, который не может быть периодическим или непрерывным. Для синусоиды с нулевым средним соотношение между среднеквадратичным значением и размахом амплитуды составляет:

От пика до пика знак равно22×RMS≈2,8×RMS.{\ displaystyle = 2 {\ sqrt {2}} \ times {\ text {RMS}} \ примерно 2,8 \ times {\ text {RMS}}.}

Для других сигналов отношения не такие же, как для синусоидальных волн. Например, для треугольной или пилообразной волны

От пика до пика знак равно23×RMS≈3.5×RMS.{\ displaystyle = 2 {\ sqrt {3}} \ times {\ text {RMS}} \ примерно 3,5 \ times {\ text {RMS}}.}

Форма волны	Переменные и операторы	RMS
ОКРУГ КОЛУМБИЯ	yзнак равноА{\ displaystyle y = A_ {0} \,}	А{\ displaystyle A_ {0} \,}
Синусоидальная волна	yзнак равноА1грех⁡(2πжт){\ Displaystyle у = А_ {1} \ грех (2 \ пи футов) \,}	А12{\ displaystyle {\ frac {A_ {1}} {\ sqrt {2}}}}
Квадратная волна	yзнак равно{А1трещина⁡(жт)<0,5-А1трещина⁡(жт)>0,5{\ displaystyle y = {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <0,5 \\ — A_ {1} & \ operatorname {frac} (ft)> 0,5 \ end {cases}} }	А1{\ Displaystyle A_ {1} \,}
Прямоугольная волна со смещением постоянного тока	yзнак равноА+{А1трещина⁡(жт)<0,5-А1трещина⁡(жт)>0,5{\ displaystyle y = A_ {0} + {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <0,5 \\ — A_ {1} & \ operatorname {frac} (ft)> 0,5 \ конец {case}}}	А2+А12{\ displaystyle {\ sqrt {A_ {0} ^ {2} + A_ {1} ^ {2}}} \,}
	yзнак равно{трещина⁡(жт)<0,25А10,25<трещина⁡(жт)<0,50,5<трещина⁡(жт)<0,75-А1трещина⁡(жт)>0,75{\ displaystyle y = {\ begin {cases} 0 & \ operatorname {frac} (ft) <0,25 \\ A_ {1} & 0,25 <\ operatorname {frac} (ft) <0,5 \\ 0 & 0,5 <\ operatorname {frac} (ft) <0,75 \\ — A_ {1} & \ operatorname {frac} (ft)> 0,75 \ end {case}}}	А12{\ displaystyle {\ frac {A_ {1}} {\ sqrt {2}}}}
Треугольник волна	yзнак равно|2А1трещина⁡(жт)-А1|{\ displaystyle y = \ left | 2A_ {1} \ operatorname {frac} (ft) -A_ {1} \ right |}	А13{\ displaystyle A_ {1} \ over {\ sqrt {3}}}
Пилообразная волна	yзнак равно2А1трещина⁡(жт)-А1{\ displaystyle y = 2A_ {1} \ operatorname {frac} (ft) -A_ {1} \,}	А13{\ displaystyle A_ {1} \ over {\ sqrt {3}}}
Пульсовая волна	yзнак равно{А1трещина⁡(жт)<Dтрещина⁡(жт)>D{\ displaystyle y = {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <D \\ 0 & \ operatorname {frac} (ft)> D \ end {cases}}}	А1D{\ displaystyle A_ {1} {\ sqrt {D}}}
Междуфазное напряжение	yзнак равноА1грех⁡(т)-А1грех⁡(т-2π3){\ displaystyle y = A_ {1} \ sin (t) -A_ {1} \ sin \ left (t — {\ frac {2 \ pi} {3}} \ right) \,}	А132{\ displaystyle A_ {1} {\ sqrt {\ frac {3} {2}}}}
где: y — смещение, т время, f — частота, A i — амплитуда (пиковое значение), D — рабочий цикл или доля периода времени (1 / f ), который был проведен на высоком уровне, гидроразрыва ( г ) является дробной частью из г .

В комбинациях сигналов

Формы сигналов, полученные путем суммирования известных простых форм сигналов, имеют среднеквадратичное значение, которое является корнем из суммы квадратов значений компонентных среднеквадратичных значений, если формы сигналов компонентов ортогональны (то есть, если среднее значение произведения одного простого сигнала на другой равно нулю. для всех пар, кроме самого времени сигнала).

RMSОбщеезнак равноRMS12+RMS22+⋯+RMSп2{\ displaystyle {\ text {RMS}} _ {\ text {Total}} = {\ sqrt {{\ text {RMS}} _ {1} ^ {2} + {\ text {RMS}} _ {2} ^ {2} + \ cdots + {\ text {RMS}} _ {n} ^ {2}}}}

В качестве альтернативы, для сигналов, которые полностью положительно коррелированы или «синфазны» друг с другом, их среднеквадратичные значения суммируются напрямую.

Что такое среднеквадратичное отклонение

Рассматривая какие-либо величины или их изменения, используют такие критерии как среднеарифметическая величина и ее отклонение. Различные понятия позволяют оценить разброс измеряемой величины и ее отклонение. К ним относится абсолютная погрешность, которая показывает насколько каждая конкретная величина отличается от среднего значения. Но так как сумма всех абсолютных погрешностей равна нулю, то этот критерий не позволяет показать разброс измеряемых величин. И для решения этой задачи был введен новый показатель — среднее квадратичное отклонение.

Для того чтобы объяснить его смысл необходимо вспомнить некоторые основные математические понятия.

Определение

Средней величиной или средним арифметическим называется число, полученное в результате деления суммы всех величин на их количество.

Пример

Среднеарифметическое для 3 чисел b₁, b₂ и b₃ определяется как:

\(M=\frac{b_1+b_2+b_3}3\)

Со средней величиной непосредственно связана и другая характеристика — математическое ожидание.

Определение

Значение среднего арифметического некоторого множества при стремлении его членов к бесконечности называется математическим ожиданием (М).

А оценкой математического ожидания является среднее арифметическое определенного числа измерений изучаемой величины.

Определение

Вариантой или абсолютной погрешностью называется разность измеряемой величины со средним значением.

Она обозначается греческой буквой D. Для того чтобы найти варианту единичного измерения ai следует отнять от ее значение среднее арифметическое:

\(Da_i=a_i-M\)

Также для оценки единичного измерения используется и относительная погрешность, значение которой выражается в процентах. Ее вычисление проводят по формуле:

\(\sigma=\frac{\left|\triangle a_i\right|}M\times100\%\)

Относительная погрешность каждой величины позволяет отбросить из вариации измерений значения с очень большой погрешностью и проводить дальнейший анализ только величин с незначительной относительной погрешностью.

Характеристикой распределения значений некоторой измеряемой величины является дисперсия (D).

Определение

Дисперсией называется среднее арифметическое квадратов всех абсолютных погрешностей.

Теперь можно дать определение и «среднеквадратичному отклонению».

Определение

Значение корня квадратного из дисперсии случайной величины называется среднеквадратичным отклонением и обозначается «ϭ».

Оно вычисляется по формуле:

\(\sigma=\sqrt{D_{\left|x\right|}}\)

Единицей измерения среднеквадратического отклонения является единица измерения исследуемой величины. Данный критерий используется при измерении линейной функции, статической проверки гипотезы, расчете стандартной ошибки среднего арифметического, а также при построении доверительных интервалов.

Архив записей

Архив записейВыберите месяц Сентябрь 2020  (1) Август 2020  (2) Июль 2020  (2) Июнь 2020  (2) Декабрь 2019  (3) Ноябрь 2019  (4) Октябрь 2019  (3) Сентябрь 2019  (2) Май 2019  (1) Октябрь 2018  (1) Июнь 2018  (1) Апрель 2018  (1) Январь 2018  (1) Ноябрь 2017  (1) Октябрь 2017  (1) Сентябрь 2017  (2) Август 2017  (4) Июль 2017  (5) Июнь 2017  (4) Май 2017  (5) Апрель 2017  (2) Март 2017  (1) Февраль 2017  (1) Январь 2017  (3) Декабрь 2016  (1) Ноябрь 2016  (2) Октябрь 2016  (3) Сентябрь 2016  (4) Август 2016  (6) Июль 2016  (9) Июнь 2016  (4) Май 2016  (5) Апрель 2016  (6) Март 2016  (5) Февраль 2016  (8) Январь 2016  (8) Декабрь 2015  (9) Ноябрь 2015  (4) Июль 2015  (1) Март 2015  (1) Февраль 2015  (1) Январь 2015  (1) Июль 2014  (1) Июль 2013  (1) Март 2013  (2) Декабрь 2012  (1) Ноябрь 2012  (1) Сентябрь 2012  (3) Август 2012  (4) Июль 2012  (4) Июнь 2012  (4) Май 2012  (4) Апрель 2012  (5) Март 2012  (7) Февраль 2012  (8) Январь 2012  (7) Декабрь 2011  (5) Ноябрь 2011  (1)

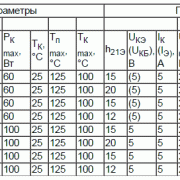
Параметры постоянного тока

Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени

• Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
  • Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
  • Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей

Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)

Среднеквадратичное значение

В зарубежной терминологии применяется аббревиатура RMS (rms) – root mean square. В математике для набора чисел x1, x2, …, xn количеством n среднеквадратичное значение (rms) определяется выражением:

Например, для чисел 2,3 и 6 среднеквадратичным значением будет квадратный корень из (2²+3²+6²)/3. √(49/3) = 4.04

Среднеквадратичным значением двух или нескольких чисел является квадратный корень из среднеарифметического значения квадратов этих чисел.

Для любой непрерывной функции в интервале T1 – T2 среднеквадратичное значение можно рассчитать по формуле:

Среднеквадратичное значение применяется в расчётах, где существует пропорциональная зависимость не самих переменных значений, а их квадратов.

Действующее значение напряжения и тока

В качестве примера можно рассмотреть квадратичную зависимость мощности или работы электрического тока от значений тока или напряжения.

P = I²R;    A = I²Rt;    P = U²/R;    A = U²t/R

Величина постоянного напряжения или тока является его среднеквадратичным значением.

Среднеквадратичное значение переменного тока равно величине постоянного тока, действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода.

Определяющим фактором здесь является среднее (среднеарифметическое) значение мощности Pavg или работы Aavg, пропорциональное квадрату значения тока.

Так же среднеквадратичное значение переменного напряжения за период равносильно по своему воздействию на активную нагрузку такому же значению постоянного напряжения.

P = UI = Pavg = UrmsIrms

Среднеквадратичное значение переменного напряжения или тока часто называют действующим или эффективным.

Примечание:Электромагнитные приборы используют для измерения переменного тока и напряжения в промышленных установках. Усилие, создаваемое измерительной катушкой в электромагнитном приборе, пропорционально квадрату тока, поэтому не меняется по направлению.

Угол отклонения стрелки определится некоторым средним усилием F, которое будет пропорционально среднеквадратичному значению тока.

Расчёт действующего значения

В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.

Запишем выражение Urms с применением интеграла функции U = Uampsin(t) для одного периода 2π : Показать расчёт Скрыть расчёт

Вынесем Uamp из под знака радикала.Воспользуемся табличным интегралом , перепишем и решим последнее выражение с применением формулы Ньютона-Лейбница:

Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:

В результате решения в итоге получим:

Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T для функции , представленной на рисунке:

Выразим Urms искомой функции с помощью определённого интеграла:

Показать расчётСкрыть расчёт

Используя табличный интеграл и формулу Ньютона-Лейбница, получаем:

В итоге преобразований получим:

Ток или напряжение любой сложной формы можно рассмотреть, как набор функций в пределах периода. Тогда значением RMS будет квадратный корень из среднеарифметического значения интегралов для квадрата каждой функции, ограниченной её интервалом времени в периоде.

Например, для множества функций F1(t) , F2(t) , … , Fn(t) в соответствующих им интервалах времени (0 – T1), (T1 – T2), …

, (Tn – T), составляющих период T, действующее напряжение (RMS) определится выражением:

Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже, T и U amp имеют те же расчётные величины, что и в рассмотренном случае c функцией ,а интегралы, определённые в интервалах, равных T, для квадратов используемых функций , будут иметь одно и то же значение

Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь среднеквадратичное значение .

Выразим Urms одного периода T, как квадратный корень из среднеарифметического значения интегралов, определённых в интервалах 0 – Ti и Ti – T для квадратов всех значений периода.

В результате получаем значение RMS, равное произведению амплитуды импульсов Uamp на квадратный корень из коэффициента заполнения (Ti / T).

В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.

Замечания и предложения принимаются и приветствуются!

Приложения

• В метеорологии , чтобы увидеть, насколько эффективно математическая модель предсказывает поведение атмосферы .
• В биоинформатики , то среднеквадратичное отклонение атомных положений является мерой среднего расстояния между атомами наложенных друг на друга белков .
• В , то СКО является мерой разности между кристаллической конформации лиганда конформации и док прогнозирования.
• В экономике RMSD используется для определения того, соответствует ли экономическая модель экономическим показателям . Некоторые эксперты утверждают, что RMSD менее надежен, чем относительная абсолютная ошибка.
• В экспериментальной психологии RMSD используется для оценки того, насколько хорошо математические или вычислительные модели поведения объясняют эмпирически наблюдаемое поведение.
• В ГИС RMSD является одним из показателей, используемых для оценки точности пространственного анализа и дистанционного зондирования.
• В гидрогеологии RMSD и NRMSD используются для оценки калибровки модели подземных вод.
• В области визуализации RMSD является частью пикового отношения сигнал / шум , мера, используемая для оценки того, насколько хорошо метод восстановления изображения работает по сравнению с исходным изображением.
• В вычислительной нейробиологии RMSD используется для оценки того, насколько хорошо система изучает данную модель.
• В спектроскопии ядерного магнитного резонанса белков RMSD используется как мера для оценки качества полученного пучка структур.
• Заявки на приз Netflix были оценены с использованием RMSD из нераскрытых «истинных» значений тестового набора данных.
• При моделировании энергопотребления зданий RMSE и CV (RMSE) используются для калибровки моделей по измеренным характеристикам здания.
• В рентгеновской кристаллографии RMSD (и RMSZ) используется для измерения отклонения внутренних координат молекул от значений библиотеки ограничений.

Среднеквадратичная мощность против пиковой мощности!

Сделав небольшой обзор различной продукции, вы заметите, что некоторые производители оценивают возможности своих продуктов по мощности, используя либо пиковую мощность в ваттах, либо ее среднеквадратичное значение, в то время как большинство используют оба значения. Например, один товар может быть оценен в 150 Вт, в то время как другая марка может иметь значение в 75 Вт.

На первый взгляд, можно подумать, что первый вариант лучше, потому что он рассчитан на более высокий уровень мощности, чем второй. Однако при ближайшем рассмотрении вы можете заметить, что первый продукт рассчитан на пиковую мощность, а второй рекламирует среднеквадратичную мощность. Как правило, пиковая мощность энергопотребления устройства в два раза превышает среднюю среднеквадратичную мощность, что в основном означает, что вышеуказанные продукты фактически имеют одинаковую мощность: пиковая 150 Вт / среднеквадратичная 75 Вт.

Однако большинство производителей аудио оборудования предпочитают уделять больше внимания максимальной пиковой мощности, чтобы для пользователя продукты выглядели так, как будто они могут «выдать» намного больше, чем они реально способны. Хотя это может звучать убедительно, но работа звукового оборудования на пиковой мощности не только бесит ваших соседей, но и выводит из строя вашу аудиосистему, требуя замены некоторых частей или покупки нового устройства в целом

Таким образом, если вы
хотите, чтобы ваша музыкальная колонка прослужил долгие годы, то стоит обратить внимание на среднеквадратичную мощность, потребляемую мощность, и ту, с которой вы хотите наслаждаться музыкой

Тем не менее, когда дело доходит до этих технических деталей, не смущайтесь номинальной мощностью колонок и характеристиками усилителя. Усилители генерируют мощность в аудиосистеме, что не относится к динамикам и сабвуферам. Поэтому значения мощности колонок относятся к количеству мощности, которое ваши колонки могут обрабатывать от усилителя. С другой стороны, характеристики усилителя относятся к тому, сколько мощности он может выдавать для максимальной производительности звука.

Практическое применение

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Экономика и финансы

Среднее квадратическое отклонение доходности портфеля σ=DX{\displaystyle \sigma ={\sqrt {D}}} отождествляется с риском портфеля.

В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.

Климат

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

Выводы

Среднеквадратическое отклонение — очень важный инструмент не только применительно к среднему времени обработки вызовов в целом по контакт-центру. Вы можете вычислить его для звонков только строго определенных типов, для вызовов по направлениям бизнеса, который обслуживает контакт-центр, или, например, только для новых сотрудников. Этот метод можно также использовать для обработки других статистических данных, которые в избытке накапливаются в любом контакт-центре. Ведь обычные средние значения не смогут описать все, что происходит.

Просто попробуйте, и вы наверняка убедитесь, что в расчете среднеквадратичного отклонения нет ничего сложного. Зато эти данные окажут вам огромную помощь в тонкой настройке бизнес-процессов в контакт-центре.

См. также:

• Доступны для заказа новые беспроводные гарнитуры Plantronics для платформ Unified Communications
• Plantronics анонсировала усовершенствованные звуковые процессоры серии MDA400 QD
• Контакт-центр будущего: как искусственный интеллект измени работу операторов